Решение задач линейного программирования в MS Excel
Инструментом для решений задач оптимизации в MS Excel служит надстройка «Поиск решения». Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках.
Если данная надстройка установлена, то «Поиск решения»запускается из меню «Сервис». Если такого пункта нет, следует выполнить команду «Сервис - Надстройки...» и выставить флажок против надстройки «Поиск решения».
Решение задачи оптимизации состоит из трёх этапов.
A. Создание модели задачи оптимизации.
B. Поиск решения задачи оптимизации.
C. Анализ найденного решения задачи оптимизации.
Рассмотрим подробнее эти этапы.
Этап А.
На этапе создания модели вводятся обозначения неизвестных, на рабочем листе заполняются диапазоны исходными данными задачи, вводится формула целевой функции.
Этап В.
Команда «Сервис - Поиск решения» открывает диалоговое окно «Поиск решения», в котором, в свою очередь, имеются следующие поля:
«Установить целевую ячейку» - служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу.
«Равной» - служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). Чтобы установить число, введите его в поле.
«Изменяя ячейки» - служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле «Установить целевую ячейку».
«Предположить» - используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле «Установить целевую ячейку». Результат поиска отображается в поле «Изменяя ячейки».
«Ограничения» - служит для отображения списка граничных условий поставленной задачи.
«Добавить» - служит для отображения диалогового окна «Добавить ограничение».
«Изменить» - служит для отображения диалоговое окна «Изменить ограничение».
«Удалить» – служит для снятия указанного ограничения.
«Выполнить» – служит для запуска поиска решения поставленной задачи.
«Закрыть» - служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки сделанные в окнах диалога, появлявшихся после нажатий на кнопки «Параметры, Добавить, Изменить или Удалить».
«Параметры» - служит для отображения диалогового окна «Параметры поиска решения», в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения.
«Восстановить» - служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
Для решения задачи оптимизации выполните следующие действия.
1. В меню «Сервис» выберите команду «Поиск решения».
2. В поле «Установить целевую ячейку» введите адрес или имя ячейки, в которой находится формула оптимизируемой модели.
3. Чтобы максимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение, соответствующее максимальному значению.
Чтобы минимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение соответствующее минимальному значению.
Чтобы установить значение в целевой ячейке равным некоторому числу путем изменения значений влияющих ячеек, установите переключатель в положение значению и введите в соответствующее поле требуемое число.
4. В поле «Изменяя ячейки» введите имена или адреса изменяемых ячеек, разделяя их запятыми. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. Допускается установка до 200 изменяемых ячеек.
Чтобы автоматически найти все ячейки, влияющие на формулу модели, нажмите кнопку «Предположить».
5. В поле «Ограничения» введите все ограничения, накладываемые на поиск решения.
6. Нажмите кнопку «Выполнить».
Чтобы восстановить исходные данные, установите переключатель в положение «Восстановить исходные значения».
Этап С.
Для вывода итогового сообщения о результате решения используется диалоговое окно «Результаты поиска решения».
Диалоговое окно «Результаты поиска решения» содержит следующие поля:
«Восстановить исходные значения» - служит для восстановления исходных значений влияющих ячеек модели.
«Отчеты» - служит для указания типа отчета, размещаемого на отдельном листе книги.
«Результаты» - используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.
«Устойчивость» - используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле (поле «Установить целевую ячейку», диалоговое окно «Поиск решения») или в формулах ограничений.
«Ограничения» - используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.
«Сохранить сценарий» - служит для отображения диалогового окна Сохранение сценария, в котором можно сохранить сценарий решения задачи, чтобы использовать его в дальнейшем с помощью диспетчера сценариев MS Excel.
Одной из возможных задач и моделей линейной оптимизации является задача о планировании производства.
Предприятие должно производить изделия видов: ,
причем количество каждого выпускаемого изделия не должно превысить спрос и одновременно не должно быть меньше запланированных величин соответственно. На изготовление изделий идет m
видов сырья ,
запасы которых ограничены соответственно величинами ![]() Известно, что на изготовление i
-ro изделия идет единиц j
-го сырья. Прибыль, получаемая от реализации изделий равна соответственно .
Требуется так спланировать производство изделий, чтобы прибыль была максимальной и при этом выполнялся план на производство каждого изделия, но не превышался спрос на него.
Известно, что на изготовление i
-ro изделия идет единиц j
-го сырья. Прибыль, получаемая от реализации изделий равна соответственно .
Требуется так спланировать производство изделий, чтобы прибыль была максимальной и при этом выполнялся план на производство каждого изделия, но не превышался спрос на него.
Лабораторная работа "Использование средства Поиск решения"
Задание:
Решить в Excel все приведенные ниже задачи (каждую на отдельном листе) и сохранить решения в файле LAB4.xls на своем пользовательском диске.
Задача 1 1
Решение задачи линейного программирования с помощью EXCEL. 2
Задача 2 4
Задача планирования производства красок 4
Задача 3 5
Решение транспортной задачи с помощью средства Поиск решения 5
Задача 1
Задача распределения ресурсов.
Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования.
Например:
Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведена ниже.Составим математическую модель, для чего введем следущие обозначения:
x j - количество выпускаемой продукции j-го типа, j=1,4 ;
b i - количество располагаемого ресурса i-го вида, i=1,3 ;
a ij - норма расхода i-го ресурса для выпуска единицы продукции j-го типа;
c j - прибыль, получаемая от реализации единицы продукции j-го типа.
Теперь приступим к составлению модели.
Для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 6 х 1 единиц сырья, где х 1 - количество выпускаемой продукции Прод1. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:
6х 1 +5х 2 +4х 3
В этом ограничении левая часть равна величине потребного ресурса, а правая показывает количество имеющегося ресурса. Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:
F=60x 1 +70x 2 +120x 3 +130x 4 --> max
x 1 +x 2 +x 3 +x 4
6x 1 +5x 2 +4x 3 +3x 4
4x 1 +6x 2 +10x 3 +13x 4
x j >=0; j=1,4
Решение задачи линейного программирования с помощью EXCEL.
1
.
Сделать активной ячейку F6.
2. Мастер функций Математические СУММПРОИЗВ на жмите кнопку Далее. На экране диалоговое окно

3. Введите зависимости для левых частей ограничений.
Работа в диалоговом окне Поиск решения.
1
.
Сервис, Поиск решения...
2 . Курсор в поле Установить целевую ячейку и введите адрес F6.
3 . Введите направление целевой функции: Максимальному значению .
4 . Курсор в поле Изменяя ячейки и введите адреса B3:E3
5. Нажмите кнопку Добавить... и в ведите граничные условия на переменные
6. После ввода ограничений, нажмите кнопку Выполнить . В результате вычислений в ячейках В3:Е3, будут отражены найденные числовые значения х i , а в ячейке F6 – значение целевой функции.
Т.О, видно, что в оптимальном решении Прод1=В3=10, Прод2=С3=0, Прод3=D3=6, Прод4=Е3=0.
При этом максимальная прибыль будет составлять F6=1320 , количество использованных ресурсов равно трудовых=F9=16, сырья=F10=84, финансов=F11=100.


С помощью диалогового окна Результат поиска решения. Решение найдено можно получить отчеты трех типов: результаты, устойчивость, пределы.
Задача 2
Задача планирования производства красок
Для производства красок для наружных и внутренних работ используют два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн, соответственно.
Суточный спрос на краску для внутренних работ никогда не превышает спроса на краску для наружных работ более чем на 1т.
Спрос на краску для внутренних работ не превышает 2т. в сутки.
Оптовые цены одной тонны красок равны: 3000 руб. для краски для наружных работ и 2000 руб. для краски для внутренних работ .
Какое количество краски каждого вида следует производить, чтобы доход от реализации был максимальным?
Расходы продуктов А и В на 1т. приведены в таблице:
|
исходный продукт |
расход исходных продуктов на тонну краски |
максимально возможный запас |
|
|
для внутренних работ |
для наружных работ |
||
х 1 - суточный объем производства краски для внутренних работ
х 2 - суточный объем производства краски для наружных работ
f -суммарная суточная прибыль от производства обоих видов красок (целевая функция)
f = 3000х 1 +2000х 2
Определить при каких допустимых значениях х 1 и х 2 значение f - максимальное
Ограничения:
Решение задачи в Excel
|
Переменные |
|||
|
Целевая функция: |
3000*А3+2000*В3 |
||
|
Ограничения |
|||
Выполните: Cервис, Поиск решения
Целевая ячейка С4
Установить: М аксимальному значению
Изменяемые ячейки: А3:В3
Ограничения:
После ввода данных нажмите кнопку Выполнить
Полученное решение:
|
Переменные |
|||
|
Целевая функция: |
|||
|
Ограничения: |
|||
Вывод: оптимальным является производство 3,3 т. краски для наружных работ и 1,3 т. краски для внутренних работ в сутки. Этот объем принесет прибыль 12,7 тыс. руб.
Задача 3
Решение транспортной задачи с помощью средства Поиск решения
Фирма имеет четыре фабрики: А, В, С, D и пять центров распределения ее товаров: №1, №2, №3, №4, №5.
Производственные возможности фабрик соответственно составляют:
А – 200, В – 150, С – 225, D – 175 единиц продукции ежедневно.
Потребности центров распределения соответственно составляют:
№1 – 100, №2 – 200, №3 – 50, №4 – 250, №5 – 150 единиц продукции ежедневно.
Хранение на фабрике единицы продукции, не поставленной в центр распределения, составляет $0,75 в день.
Штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день.
Стоимость перевозки единицы продукции с фабрик в пункты распределения представлена в таблице:
Спланировать перевозки так, чтобы минимизировать суммарные транспортные расходы.
Модель рассматриваемой задачи сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), значит не нужно учитывать издержки, связанные как со складированием, так и с недопоставками продукции. В противном случае в модель следует ввести:
В случае перепроизводства – фиктивный пункт распределения, стоимость перевозок единицы продукции, в который полагается равной стоимости складирования, а объемы перевозок – объемам складирования излишков продукции на фабриках.
В случае дефицита – фиктивную фабрику, стоимость перевозок единицы продукции с которой полагается равной стоимости штрафов за недопоставку продукции, а объемы перевозок – объемам недопоставок продукции в пункты распределения.
x ij – объем перевозок с i-й фабрики в j-й центр распределения.
c ij – стоимость перевозки единицы продукции с i-й фабрики в j-й центр распределения.
а i – объем производства на i-й фабрике.
в j – спрос в j-м центре распределения.
Т
ребуется
минимизировать суммарные транспортные
расходы, т.е.
Ограничения:
x


ij
0 , i
, j
Механизм решения задачи в Excel с использованием средства Поиск решения
В ячейки А1:Е4 введите стоимости перевозок.
А6:Е9 – отведите под значения неизвестных (объемы перевозок).
В ячейки G6:G9 введите объемы производства на фабриках.
В А11:Е11 – потребность в продукции в пунктах распределения.
В ячейку F10 – введите целевую функцию
В А10:Е10 –введите формулы, определяющие объем продукции, ввозимой в центры распределения
В F6: F9 – формулы, вычисляющие объем продукции, вывозимой с фабрик.
|
СУММ(A6:E6) |
|||||||
|
СУММ(A7:E7) |
|||||||
|
СУММ(A8:E8) |
|||||||
|
СУММ(A9:E9) |
|||||||
|
СУММ(A6:A9) |
СУММ(B6:B9) |
СУММ(C6:C9) |
СУММ(D6:D9) |
СУММ(E6:E9) |
СУММПРОИЗВ(A1:E4;A6:E9) |
||
Сервис Поиск решения
В
окне диалога Поиск решения:
Установить
целевую ячейку $F$10
Равной
мин
имальному
значению
Изменяя
ячейки:
$А$6:$E$9
Ограничения:
$А$10:$E$10=$A$11:$E$11
$А$6:$E$9>=0
$F$6:$F$9=$G$6:$G$9
Щелкните на кнопке Параметры… и установите флажок Линейная модель
Нажмите кнопку Выполнить
Оптимальное решение транспортной задачи будет отражено в диапазоне А6:Е9
Решите транспортную задачу самостоятельно, используя выше описанный механизм.
|
Excel необходимо: ... Задачи линейного программирования. Графический метод решения задач линейного программированияРешениеMicrosoft Excel . Решение задач выпуклого программирования при помощи линейной аппроксимации. Приближённое решение задач математического программирования методом сепарабельного программирования . Экономические задачи , решаемые с помощью ... Инструкция по использованию microsoft Excel для решения задач лп 5 3 Одноиндексные задачи лп 6 > 3 Ввод исходных данных 6 > 3 Решение задачи 13Инструкция1. ЛАБОРАТОРНАЯ РАБОТА №1 “РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel ” 1.1. ЦЕЛЬ РАБОТЫ Приобретение навыков решения задач линейного программирования (ЛП) в табличном... Некоторые понятия линейного программированияДокументМы приведем решение этой задачи с помощью программы Tora. рассмотрим реализацию задачи линейного программирования в... задачи с помощью Microsoft Excel . 1. Осуществляем ввод данных в таблицу Excel (рис. 1). Рис. 1. Заполнение листа для решения задачи ... |
Рассмотрим пример задачи линейного программирования.
Требуется определить, в каком количестве надо выпустить продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 1.
| Ресурс | Прод1 | Прод2 | Прод3 | Прод4 | Знак | Наличие |
| Прибыль | ||||||
| Трудовые | ||||||
| Сырье | ||||||
| Финансы |
Рисунок 1.
Математическая модель задачи имеет вид:
где x j – количество выпускаемой продукции j-го типа; F – функция цели; в левых частях выражений ограничений указаны величины потребного ресурса , а правые части показывают количество имеющегося ресурса .
Ввод условий задачи
Для решения задачи с помощью Excel следует создать форму для ввода исходных данных и ввести их. Форма ввода показана на рис. 2.
В ячейку F6 введено выражение целевой функции как суммы произведений значений прибыли от выпуска единицы продукции каждого типа на количество выпускаемой продукции соответствующего типа. Для наглядности на рис. 3 представлена форма ввода исходных данных в режиме вывода формул.
В ячейки F8:F10 введены левые части ограничений для ресурсов каждого вида.

Рисунок 2.

Рисунок 3.
Решение задачи линейного программирования
Для решения задач линейного программирования в Excel используется мощный инструмент, называемый Поиск решения . Обращение к Поиску решения осуществляется из меню Сервис , на экран выводится диалоговое окно Поиска решения (рис. 4).

Рисунок 4.
Ввод условий задачи для поиска ее решения состоит из следующих шагов:
1 Назначить целевую функцию, для чего установить курсор в поле Установить целевую ячейку окна Поиск решения и щелкнуть в ячейке F6 в форме ввода;
2 Включить переключатель значения целевой функции, т.е. указать ее Равной Максимальному значению ;
3 Ввести адреса изменяемых переменных (x j): для этого установить курсор в поле Изменяя ячейки окна Поиск решения, а затем выделить диапазон ячеек B3:E3 в форме ввода;
4 Нажать кнопку Добавить окна Поиск решения для ввода ограничений задачи линейного программирования; на экран выводится окно Добавление ограничения (рис. 5) :
Ввести граничные условия для переменных x j (x j ³0), для этого в поле Ссылка на ячейку указать ячейку В3, соответствующую х 1 , выбрать из списка нужный знак (³), в поле Ограничение указать ячейку формы ввода, в которой хранится соответствующее значение граничного условия, (ячейка В4), нажать кнопку Добавить ; повторить описанные действия для переменных х 2 , х 3 и х 4 ;
Ввести ограничения для каждого вида ресурса, для этого в поле Ссылка на ячейку окна Добавление ограничения указать ячейку F9 формы ввода, в которой содержится выражение левой части ограничения, наложенного на трудовые ресурсы, в полях Ограничение указать знак £ и адрес Н9 правой части ограничения, нажать кнопку Добавить ; аналогично ввести ограничения на остальные виды ресурсов;
После ввода последнего ограничения вместо Добавить нажать ОК и возвратиться в окно Поиск решения.

Рисунок 5.
Решение задачи линейного программирования начинается с установки параметров поиска:
В окне Поиск решения нажать кнопку Параметры , на экран выводится окно Параметры поиска решения (рис. 6);
Установить флажок Линейная модель, что обеспечивает применение симплекс-метода;
Указать предельное число итераций (по умолчанию – 100, что подходит для решения большинства задач);
Установить флажок , если необходимо просмотреть все этапы поиска оптимального решения;
Нажать ОК , возврат в окно Поиск решения .

Рисунок 6.
Для решения задачи нажать кнопку Выполнить в окне Поиск решения , на экране – окно Результаты поиска решения (рис. 7), в котором содержится сообщение Решение найдено. Все ограничения и условия оптимальности выполнены. Если условия задачи несовместны, то выводится сообщение Поиск не может найти подходящего решения . Если целевая функция не ограничена, то появляется сообщение Значения целевой ячейки не сходятся .

Рисунок 7.
Для рассматриваемого примера решение найдено и результат оптимального решения задачи выводится в форме ввода: значение целевой функции, соответствующее максимальной прибыли и равное 1320, указывается в ячейке F6 формы ввода, оптимальный план выпуска продукции х 1 =10, х 2 =0, х 3 =6, х 4 =0 указывается в ячейках В3:С3 формы ввода (рис. 8).
Количество использованных для выпуска продукции ресурсов выводится в ячейки F9:F11: трудовых – 16, сырья – 84, финансов – 100.

Рисунок 8.
Если при установке параметров в окне Параметры поиска решения (рис. 6) был установлен флажок Показывать результаты итераций , то будут показаны последовательно все шаги поиска. На экран будет выводиться окно (рис. 9). При этом текущие значения переменных и функции цели будут показаны в форме ввода. Так, результаты первой итерации поиска решения исходной задачи представлены в форме ввода на рисунке 10 .

Рисунок 9.

Рисунок 10.
Чтобы продолжить поиск решения, следует нажимать кнопку Продолжить в окне Текущее состояние поиска решения .
Анализ оптимального решения
Прежде чем, перейти к анализу результатов решения, представим исходную задачу в форме
введя дополнительные переменные у i , представляющие собой величины неиспользованных ресурсов.
Составим для исходной задачи двойственную задачу и введем дополнительные двойственные переменные v i .
Анализ результатов поиска решения позволит увязать их с переменными исходной и двойственной задач.
С помощью окна Результаты поиска решения можно вызвать отчеты трех типов, позволяющие анализировать найденное оптимальное решение:
Результаты,
Устойчивость,
Пределы.
Для вызова отчета в поле Тип отчета выделить название нужного типа и нажать ОК .
1 Отчет по результатам (рис. 11) состоит из трех таблиц:
Таблица 1 содержит сведения о целевой функции; в столбце Исходно указывается значение целевой функции до начала вычислений;
Таблица 2 содержит значения искомых переменных x j , полученных в результате решения задачи (оптимальный план выпуска продукции);
Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для Ограничений в графе Формула приведены зависимости, которые были введены при задании ограничений в окне Поиск решения ; в графе Значение указаны величины использованного ресурса; в графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние выводится сообщение связанное ; при неполном использовании ресурса в этой графе указывается не связан. Для Граничных условий приводятся аналогичные величины с той лишь разницей, что вместо неиспользованного ресурса показана разность между значением переменной x j в найденном оптимальном решении и заданным для нее граничным условием (x j ³0).
Именно в графе Разница можно увидеть значения дополнительных переменных y i исходной задачи в формулировке (2). Здесь у 1 =у 3 =0, т.е. величины неиспользованных трудовых и финансовых ресурсов равны нулю. Эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья у 2 =26, значит, имеются излишки сырья.

Рисунок 11.
2 Отчет по устойчивости (рис. 12)состоит из двух таблиц.
В таблице 1 приводятся следующие значения:
Результат решения задачи (оптимальный план выпуска);
- Нормир. стоимость , т.е. величины, показывающие, насколько изменится целевая функция при принудительном включении единицы продукции соответствующего типа в оптимальный план;
Коэффициенты целевой функции;
Предельные значения приращения коэффициентов целевой функции, при которых сохраняется оптимальный план выпуска.
В таблице 2 содержатся аналогичные данные для ограничений:
Величины использованных ресурсов;
- Теневая цена , показывающая, как изменится целевая функция при изменении величины соответствующего ресурса на единицу;
Допустимые значения приращений ресурсов, при которых сохраняется оптимальный план выпуска продукции.

Рисунок 12.
Отчет по устойчивости позволяет позволяет получить двойственные оценки.
Как известно, двойственные переменные z i показывают, как изменится целевая функция при изменении ресурса i-го типа на единицу. В отчете Excel двойственная оценка называется Теневой ценой .
В нашем примере сырье не используется полностью и его ресурс у 2 =26. Очевидно, что увеличение количества сырья, например, до 111 не повлечет за собой увеличения целевой функции. Следовательно, для второго ограничения двойственная переменная z 2 =0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная будет больше нуля, а двойственная оценка этого ограничения равна нулю.
В рассматриваемом примере трудовые ресурсы и финансы использовались полностью, поэтому их дополнительные переменные равны нулю (у 1 =у 3 =0). Если ресурс используется полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции, и следовательно, на величину целевой функции. Двойственные оценки ограничений на трудовые и финансовые ресурсы отличны от нуля, т.е. z 1 =20, z 3 =10.
Значения двойственных оценок находим в Отчете по устойчивости , в таблице 2, в графе Теневая цена .
При увеличении (уменьшении) трудовых ресурсов на единицу целевая функция увеличится (уменьшится) на 20 единиц и будет равна
F=1320+20×1=1340 (при увеличении).
Аналогично, при увеличении объема финансов на единицу целевая функция будет
F=1320+10×1=1330.
Здесь же, в графах Допустимое увеличение и Допустимое уменьшение таблицы 2, показаны допустимые пределы изменения количества ресурсов j-го вида. Например, для при изменении приращения величины трудовых ресурсов в пределах от –6 до 3,55, как показано в таблице, структура оптимального решения сохраняется, т.е наибольшую прибыль обеспечивает выпуск Прод1 и Прод3, но в других количествах.
Дополнительные двойственные переменные также отражены в Отчете по устойчивости в графе Нормир. стоимость таблицы 1.
Если основные переменные не вошли в оптимальное решение, т.е. равны нулю (в примере х 2 =х 4 =0), то соответствующие им дополнительные переменные имеют положительные значения (v 2 =10, v 4 =20). Если же основные переменные вошли в оптимальное решение (х 1 =10, х 3 =6), то их дополнительные двойственные переменные равны нулю (v 1 =0, v 3 =0).
Эти величины показывают, насколько уменьшится (поэтому знак минус в значениях переменных v 2 и v 4) целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции вида Прод3, то целевая функция уменьшится на 10 единиц и будет равна 1320 -10×1 =1310.
Обозначим через Dс j изменение коэффициентов целевой функции в исходной модели (1). Эти коэффициенты определяют прибыль, получаемую при реализации единицы продукции j-го вида.
В графах Допустимое увеличение и Допустимое Уменьшение таблицы 1 Отчета по устойчивости показаны пределы изменения Dс j , при которых сохраняется структура оптимального плана, т.е. будет выгодно по-прежнему выпускать продукцию вида Продj. Например, при изменении Dс 1 в пределах -12£ Dс 1 £ 40, как показано в отчете, по-прежнему будет выгодно выпускать продукцию вида Прод1. При этом значение целевой функции будет F=1320+x 1 ×Dс j =1320+10×Dс j .
3 Отчет по пределам приведен на рис. 13. В нем показывается, в каких пределах могут изменяться значения x j , вошедшие в оптимальное решение, при сохранении структуры оптимального решения. Кроме этого, для каждого типа продукции приводятся значения целевой функции, получаемые при подстановке в оптимальное решение значения нижнего предела выпуска изделий соответствующего типа при неизменных значениях выпуска остальных типов. Например, если при оптимальном решении х 1 =10, х 2 =0, х 3 =6, х 4 =0 положить х 1 =0 (нижний предел) при неизменных х 2 , х 3 и х 4 , то значение целевой функции будет равно 60×0+70×0+120×6+130×0=720.

В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel , нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel » внизу окна:

Далее в открывшемся списке нужно выбрать Надстройки
, затем установить курсор на пункт Поиск решения
, нажать кнопку Перейти
и в следующем окне включить пакет анализа.

Для того чтобы решить задачу ЛП в табличном процессоре Microsoft Excel , необходимо выполнить следующие действия:
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи :
· переменных,
· целевой функции (ЦФ),
· ограничений,
· граничных условий;
b) ввести исходные данные в экранную форму :
· коэффициенты ЦФ,
· коэффициенты при переменных в ограничениях,
· правые части ограничений;
c) ввести зависимости из математической модели в экранную форму :
· формулу для расчета ЦФ,
· формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне "Поиск решения" ):
· целевую ячейку,
· направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне "Поиск решения" ):
· ячейки со значениями переменных,
· граничные условия для допустимых значений переменных,
· соотношения между правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне "Поиск решения" );
b) запустить задачу на решение (в окне "Поиск решения" ) ;
c) выбрать формат вывода решения (в окне "Результаты поиска решения" ).
Рассмотрим подробно использование MS Excel на примере решения следующей задачи.
Задача.
Фабрика "GRM pic" выпускает два вида каш для завтрака - "Crunchy" и "Chewy". Используемые для производства обоих продуктов ингредиенты в основ-ном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.
Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
|
Цех |
Необходимый фонд рабочего времени чел.-ч/т |
Общий фонд рабочего времени чел.-ч. в месяц |
|
|
"Crunchy" |
"Chewy" |
||
|
А. Производство |
10 |
4 |
1000 |
|
В. Добавка приправ |
3 |
2 |
360 |
|
С. Упаковка |
2 |
5 |
600 |
Доход от производства 1 т "Crunchy" составляет 150 ф. ст., а от производства "Chewy" - 75 ф, ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.
Требуется:
а) Сформулировать модель линейного программирования, максимизи-рующую общий доход фабрики за месяц.
б) Решить ее c помощью MS Excel.
Формальная постановка данной задачи имеет вид:
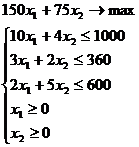 (1)
(1)
Ввод исходных данных
Создание экранной формы и ввод исходных данных
Экранная форма для решения в MS Excel представлена на рисунке 1. 
Рисунок 1.
В экранной форме на рисунке 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи 1 соответствуют ячейки B4
(), C4
(), коэффициентам ЦФ соответствуют ячейки B6
(150), C6
(75), правым частям ограничений соответствуют ячейки
D
18
(1000), D
19
(360), D
20
(600) и т.д.
Ввод зависимостей из формальной постановки задачи в экранную форму
Для ввода зависимостей определяющих выражение для целевой функции и ограничений используется функция MS Excel СУММПРОИЗВ , которая вычисляет сумму попарных произведений двух или более массивов.
Одним из самых простых способов определения функций в MS Excel является использование режима "Вставка функций",
который можно вызвать из меню "Вставка"
или при нажатии кнопки "

Рисунок 2
Так, например, выражение для целевой функции из задачи 1 определяется следующим образом:
· курсор в поле D 6;
· нажав кнопку "
· в окне "Функция"
выберитефункцию СУММПРОИЗВ
(рис. 3);

Рисунок 3
· в появившемся окне "СУММПРОИЗВ"
в строку "Массив 1"
введите выражение B
$4:
C
$4
, а в строку "Массив 2"
- выражение B
6:
C
6
(рис. 4);

Рисунок 4
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3 ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B 13, C 13 - 1-е ограничение; B 14, С14 - 2-е ограничение и B 15, С15 - 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.
Таблица 1.
Формулы, описывающие ограничения модели (1)
|
Левая часть ограничения |
Формула Excel |
|
|
=СУММПРОИЗВ(B 4: C 4; B 13: C 13)) |
|
|
=СУММПРОИЗВ(B 4: C 4; B 14: C 14)) |
|
|
=СУММПРОИЗВ(B 4: C 4; B 15: C 15) |
Задание ЦФ
Дальнейшие действия производятся в окне "Поиск решения" , которое вызывается из меню "Сервис" (рис.5):
· поставьте курсор в поле "Установить целевую ячейку" ;
· введите адрес целевой ячейки $ D $6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры;
· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению".

Рисунок 5
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно "Поиск решения"
в поле "Изменяя ячейки"
впишите адреса $
B
$4:$С$4
. Необходимые адреса можно вносить в поле "Изменяя ячейки"
и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1).
· Нажмите кнопку "Добавить" , после чего появится окно "Добавление ограничения" (рис.6).
· В поле "Ссылка на ячейку" введите адреса ячеек переменных $ B $4:$С$4 . Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
· В поле знака откройте список предлагаемых знаков и выберите .
· В поле "Ограничение"
введите 0.

Рис.6 - Добавление условия неотрицательности переменных задачи (1)
Задание знаков ограничений
,
, =
· Нажмите кнопку "Добавить" в окне "Добавление ограничения" .
· В поле "Ссылка на ячейку" введите адрес ячейки левой части конкретного ограничения, например $ B $18 . Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
· В соответствии с условием задачи (1) выбрать в поле знака необходимый знак, например, .
· В поле "Ограничение" введите адрес ячейки правой части рассматриваемого ограничения, например $ D $18 .
· Аналогично введите ограничения: $ B $19<=$ D $19 , $ B $20<=$ D $20 .
· Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK .
Окно "Поиск решения" после ввода всех необходимых данных задачи (1) представлено на рис. 5.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки "Изменить"
или "Удалить"
(см. рис. 5).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне "Поиск решения".
Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры"
и заполнить некоторые поля окна "Параметры поиска решения"
(рис. 7).

Рис. 7 - Параметры поиска решения, подходящие для большинства задач ЛП
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр "Сходимость" применяется только при решении нелинейных задач.Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки "
OK
"
.
Запуск задачи на решение
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".
После запуска на решение задачи ЛП на экране появляется окно "Результаты поиска решения"
с сообщением об успешном решении задачи, представленном на рис. 8.

Рис. 8 -. Сообщение об успешном решении задачи
Появление иного сообщения свидетельствует не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки , не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра "Относительная погрешность" не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне "Результаты поиска решения"
представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы"
. Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "
OK
".
После этого в экранной форме появляется оптимальное решение задачи (рис. 9).

Рис.9 - Экранная форма задачи (1) после получения решения
Цель работы: изучение современных программных средств решения задачи линейного программирования; практическое решение задач линейного программирования графическим методом, симплекс-методом и средствами программыMicrosoftExcel; программная реализация симплекс-метода на языке программирования высокого уровня.
1. Теоретическая часть
Для решения задач линейного программирования в программе Microsoft Excel имеется надстройка Поиск решения , обращение к которой производится из меню Сервис .
Если команда Поиск решения отсутствует в меню Сервис , то требуется установить надстройку «Поиск решения». Для этого в меню Сервис выбирается команда Надстройки , которая открывает диалоговое окно, показанное на рис. 1.
Покажем использование надстройки «Поиск решения» на примере решения следующей задачи.
Постановка задачи
Предприятие изготавливает и реализует три вида продукции – P 1 , Р 2 и Р 3 . Для производства продукции используются три вида ресурсов – комплектующие изделия, сырье и материалы. Запасы ресурсов и их расход на изготовление единицы продукции каждого вида приведены в табл. 1.
Таблица 1
Прибыль от реализации единицы продукции каждого вида составляет 240, 210 и 180 денежных единиц для P 1 , Р 2 и Р 3 соответственно.
Требуется определить производственную программу предприятия таким образом, чтобы прибыль от реализации продукции была максимальной.
Математическая модель задачи
Обозначим переменными x 1 , x 2 и x 3 искомые объемы производства продукции видов P 1 , Р 2 и Р 2 , а через F – прибыль предприятия. Тогда математическая постановка представленной задачи принимает следующий вид.
Определить значения переменных x 1 , x 2 и x 3 , для которых достигается максимум целевой функции
F = 240 x 1 + 210 х 2 + 180 x 3
при ограничениях:

Целевая функция описывает суммарную прибыль от реализации произведенной продукции всех трех видов. Ограничения (1), (2) и (3) учитывают расход и запасы комплектующих изделий, сырья и материалов соответственно. Поскольку объемы производства продукции не могут быть отрицательными, добавляются условия
x 1 ≥ 0; x 2 ≥ 0; x 3 ≥ 0.
Порядок оптимального решения задачи
Примерные действия, необходимые для решения задачи линейного программирования средствами программы Excel, представим в виде последовательности шагов.
Шаг 1. Исходные данные задачи записываются на рабочем листе электронной таблицы. Один из вариантов показан на рис. 2.

Замечание. Если известно исходное допустимое базисное решение, то можно несколько ускорить процесс поиска оптимального решения. Для этого начальные значения некоторых или всех переменных могут быть заданы вручную. В данном примере для их хранения используются ячейки $B$2, $C$2 и $D$2. Если допустимое базисное решение не задано, то программа Excel автоматически определяет начальные значения переменных задачи.
Шаг 2. В ячейку E3 вводится формула
СУММПРОИЗВ(В3:D3; $B$2:$D$2)
для вычисления текущего значения целевой функции, которая находит сумму попарных произведений ячеек (В3:D3) с коэффициентами при переменных в выражении целевой функции на ячейки ($B$2:$D$2) с текущими значениями переменных.
Шаг 3. Чтобы задать ограничения решаемой задачи, в ячейки E5, E6 и E7 копируется формула из ячейки E3. После этого в указанных ячейках должны быть получены формулы, представленные в табл. 2.
Таблица 2
|
СУММПРОИЗВ(В5:D5; $B$2:$D$2) |
|
|
СУММПРОИЗВ(В6:D6; $B$2:$D$2) |
|
|
СУММПРОИЗВ(В7:D7; $B$2:$D$2) |
Шаг 4. После создания таблицы с исходными данными курсор устанавливается в ячейку E3, содержащую формулу для вычисления целевой функции. Далее в меню Сервис выбирается команда Поиск решения , которая открывает диалоговое окно, приведенное на рис. 3.

В поле Установить целевую ячейку окна «Поиск решения», показанного на рис. 3, должен появиться адрес ячейки с формулой целевой функции (в данном примере это ячейка $E$3).
Затем в этом окне (рис. 3) заполняются следующие поля этого окна:
В поле Равной переключатель вида экстремума целевой функции устанавливается в положение максимальное значение (или минимальное значение при соответствующей постановке задачи);
В поле Изменяя ячейки указывается диапазон ячеек со значениями переменных задачи, выделяемый на рабочем листе электронной таблицы (в примере это ячейки $B$2:$D$2);
В поле Ограничения задаются ограничения исходной задачи. Для этого курсор устанавливается в поле ввода ограничений и нажимается кнопка Добавить . В результате выводится диалоговое окно «Добавление ограничения», показанное на рис. 4.

В этом окне в поле Ссылка на ячейку вводится адрес ячейки с формулой соответствующего ограничения (например, для ограничения (1) это будет ячейка E5), а в поле Ограничение указывается предельное значение, которое может принимать выбранное ограничение (в данном примере правая часть ограничения (1) находится в ячейке G5).
Следует заметить, что заполнение полей Ссылка на ячейку и Ограничение в окне «Добавление ограничения» можно выполнить выделением соответствующих ячеек рабочего листа электронной таблицы.
Затем выбирается вид отношения, связывающего левую и правую части ограничения, что показано на рис. 5.

После нажатия кнопки Добавить в окне «Добавление ограничения» (или кнопки ОК для ввода последнего ограничения) данное ограничение попадает в список ограничений решаемой задачи. С помощью кнопок Удалить и Изменить можно удалять выделенные в списке ограничения или вносить в них исправления.
Замечание . В окне «Добавление ограничения» можно указать, что все или некоторые переменные должны принимать только целые значения (рис. 5). Это позволяет получать решения задач целочисленного линейного программирования (полностью или частично целочисленных).
Шаг 5. После заполнения всех полей окна «Поиск решения» нажимается кнопка Параметры (рис. 3), которая открывает диалоговое окно «Параметры поиска решения», показанное на рис. 6.

В этом окне требуется установить флажки Линейная модель для решения задачи линейного программирования и Неотрицательные значения , если такое условие накладываются на все переменные задачи.
Здесь (рис. 6) также можно определить параметры процесса решения: предельное время поиска решения, максимальное количество итераций, точность и т.п. Флажок Показывать результаты итераций позволяет по шагам следить за поиском решения. Флажок Автоматическое масштабирование включается в том случае, когда разброс значений переменных очень велик.
Шаг 6. Задав необходимые параметры в окне «Параметры поиска решения», следует нажать на кнопку Выполнить для поиска решения задачи (рис. 3) в окне «Поиск решения». Если решение найдено, то на экран выводится окно с соответствующим сообщением (рис. 7).

Полученные результаты отображаются на рабочем листе электронной таблицы, как это показано на рис. 8. В частности, значения переменных - в ячейках $B$2:$D$2, значение целевой функции – в ячейке E3.

Таким образом,
получено оптимальное решение исходной
задачи в виде вектора
 ,
где
,
где ,
, и
и ,
для которого значение целевой функцииF
максимально и составляет F
*
= 129825.
,
для которого значение целевой функцииF
максимально и составляет F
*
= 129825.
Результаты решения задачи линейного программирования также можно сохранить в виде отдельных рабочих листов с именами Отчет по результатам , Отчет по устойчивости и Отчет по пределам . Для сохранения результатов в виде отчетов необходимо предварительно в поле Тип отчета выделить требуемые типы отчетов (рис. 7). В этом же окне можно отказаться от полученных решений и восстановить исходные значения переменных.
Отчет по результатам для рассмотренной задачи показан на рис. 9.

В данном отчете
представлены оптимальное решение задачи
линейного программирования и его
расположение в области допустимых
решений. В графах Результат
выводятся
оптимальные значения целевой функции
F
*
и переменных задачи
 ,
а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение
).
Состояние
ограничений (графа Статус
)
характеризует расположение точки
,
а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение
).
Состояние
ограничений (графа Статус
)
характеризует расположение точки
 в области допустимых решений. ГрафаРазница
показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки
в области допустимых решений. ГрафаРазница
показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки
 на границе области допустимых решений,
которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
на границе области допустимых решений,
которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
Замечание . В экономической интерпретации связанные ограничения соответствуют дефицитным ресурсам. Для не связанных ограничений графа Разница показывает оставшиеся объемы неиспользованных не дефицитных ресурсов. В рассмотренной задаче ограничения (1) и (3) соответствуют комплектующим изделиям и материалам, которые являются дефицитными ресурсами. Ограничение (2) является не связанным, т.е. не влияет на оптимальный план производства продукции по критерию максимальной прибыли. Это означает, что второй ресурс (сырье) не использован в объеме 292,5 ед.
В отчете по устойчивости (рис. 10) приведены границы устойчивости переменных задачи (графы Допустимое увеличение и Допустимое уменьшение коэффициентов целевой функции), а также границы устойчивости теневых цен (т.е. переменных двойственной задачи), в пределах которых оптимальное решение не изменяется. Большие значения пределов (1Е+30) означают фактическое отсутствие соответствующих границ, т.е. переменная может изменяться до бесконечности.

В графе Нормированная стоимость элемент во второй строке (-150) показывает, на сколько уменьшится значение функции, если в решении переменную x 2 увеличить на единицу. С другой стороны, при допустимом увеличении коэффициента функции при неизвестной x 2 на 150 единиц значение этой переменной не изменится, т.е. неизвестная x 2 будет равна нулю, а если выйти за пределы допустимого увеличения (коэффициент при x 2 увеличить более чем на 150), то неизвестная x 2 в решении будет больше нуля.
В отчете по пределам (рис. 11) показаны нижние и верхние пределы возможного изменения переменных (в пределах области допустимых решений) и соответствующие значения целевой функции (графа Целевой результат ) при этих изменениях. В частности, если x 1 = 0, а x 2 и x 3 остаются без изменений, то F = 2400 + 2100 + 180191,25 = 34425; при x 3 = 0 и неизменных x 1 и x 2 получим F = 240397,5 + 2100 + 1800 = 95400.